:: Projekte :: Fractal ::

Fractal

Mandelbrot

Der Begriff Fraktal wurde von Benoit Mandelbrot geprägt und ist durch das "Apfelmännchen" berühmt geworden. Interessant an der Sache ist die recht einfach aussehende Definition der Mandelbrotmenge, deren grafische Darstellung das "Apfelmännchen" ergibt. Die folgende Abbildung zeigt ein "Apfelmännchen":

Definiert wird die Mandelbrotmenge M über die Menge der komplexen Zahlen c, z(i) und der rekursiven Definition: z(n+1)= z(n)^2+c, wobei der Anfangswert z(0)=0 ist.
Zu der grafischen Darstellung der Menge kommt man, indem man die Konvergenz der einzelnen Werte der Menge untersucht und für den Grad der Konvergenz eine Farbe aufträgt.
Erstaunlich ist, daß mit einem sehr kleinen Code-Schnipsel der Grat der Konvergenz und damit die Mandelbrot-Menge berechnet werden kann. Die folgenden Zeilen zeigen dies:
01 public int checkFast(double ci, double c) { 02 double zi = 0; 03 double z = 0; 04 for(int i=0;i<DEEP;i++) { 05 double ziT = 2*(z*zi); 06 double zT =z*z-(zi*zi); 07 z = zT + c; 08 zi = ziT + ci; 09 10 if(z*z + zi*zi >= 4.0) { 11 return i; 12 } 13 } 14 return DEEP; 15 } Zu beachten sind die Zeilen 05 und 06. Dort werden die Rechenregeln für die komplexen Zahlen umgesetzt. D.h. (zi+z)^2 = (xi)^2 + 2(zi+z) + z^2. Wobei ja gilt i^2=-1. Also erhält man: 2*(z+zi) und z*z - zi*zi. Die Ergebnisse der Rechnung werden in temporären Variablen gehalten (Es hätte auch eine Variable ausgereicht). In den Zeilen 07 und 08 wird der reelle und imaginäre Anteil jeweils addiert, wie in der rekursiven Definition festgelegt. DEEP gibt an, bis zur welcher Tiefe die Folge auf Konvergenz untersucht werden soll.
Besonders interessant ist die Abbruchbedingung in Zeile 10. Es wird davon ausgegangen, daß eine Folge divergiert, wenn das Quadrat des Betrags von z(n) größer als 4 ist. Wenn man diese Bedingung durch eine Implementierung ersetzt, die immer zwei aufeinanderfolgende z(n) auf Änderung untersucht (mit einem definierten Epsilon), erhält man ein Fraktal, das einem Apfel schon ähnlicher sieht. Eine möglich Implementierung ist im Folgenden zu sehen:
public int checkConvergence(double ci, double cr) { double zi = 0; double z = 0; double zi_LAST = 0; double z_LAST = 999; for(int i=0;i<DEEP;i++) { if(equal(zi, z, zi_LAST, z_LAST)) { return i; } zi_LAST = zi; z_LAST = z; double ziT = 2*(z*zi); double zT =z*z-(zi*zi); z = zT + cr; zi = ziT + ci; } return DEEP; } private static double fabs(double a) { if(a<0) { return -a; } return a; } public static boolean equal(double xi, double x, double yi, double y) { if(fabs(x-y)<EPSILON && fabs(xi-yi)<EPSILON) { return true; } return false; }
Die passende grafische Darstellung ist in folgender Abbildung zu sehen:

Apfel

Julia

Bei der Julia-Menge ist es so, daß der Startwert z(0) nicht mit 0 belegt werden muß, d.h. die komplexe Zahl kann verändert werden. Es ist also möglich den real- und den imaginär-Teil der komplexen Zahl zu variieren.
Durch diese Variationen erhält man eine Reihe von interessanten Fraktalen. Dies zeigen die folgenden Abbildungen.


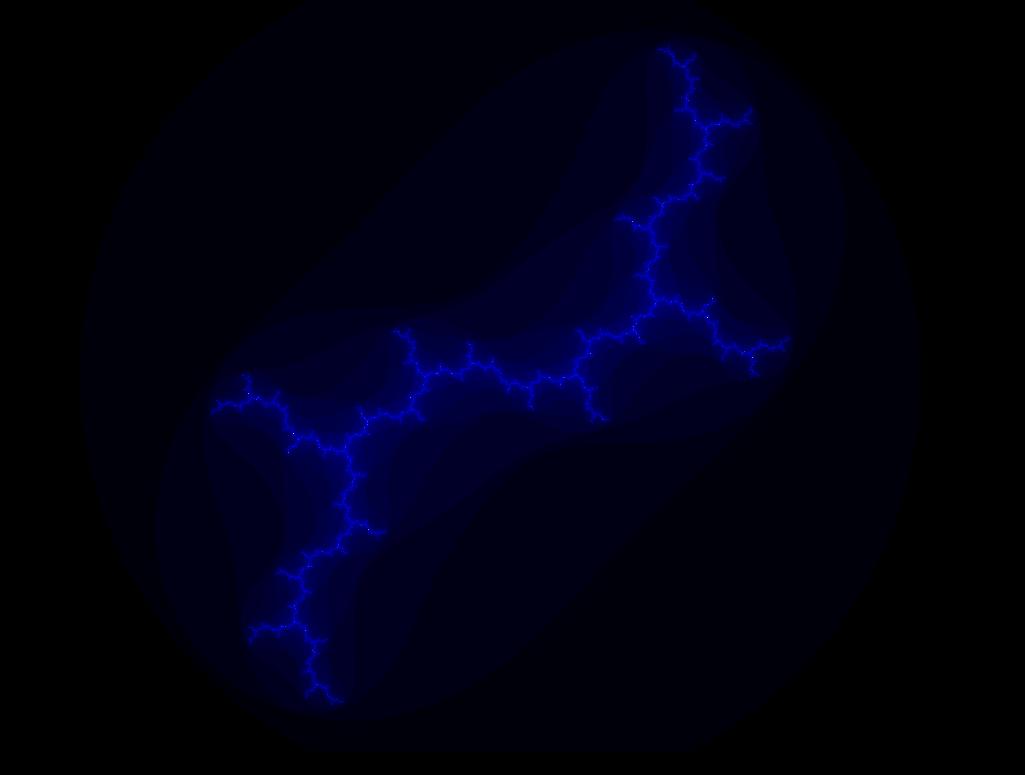1.0i+0	0.6i+0.5	0.6i-0.5

0.6i-0.4	0.5i+0.3	0.0i-1.0

Programm

Mit dem folgenden Java-Prgramm kann jeder selbst ein bißchen rumspielen und eigene Fraktale generieren. Die Oberfläche ist recht einfach zu bedienen. In einem Dialog, den man über File->New erreicht, kann man die Parameter für die Fraktale einstellen. Außerdem ist es möglich, erzeugte Fraktale mit dem Menüpunkt File->Save as..., zu speichern.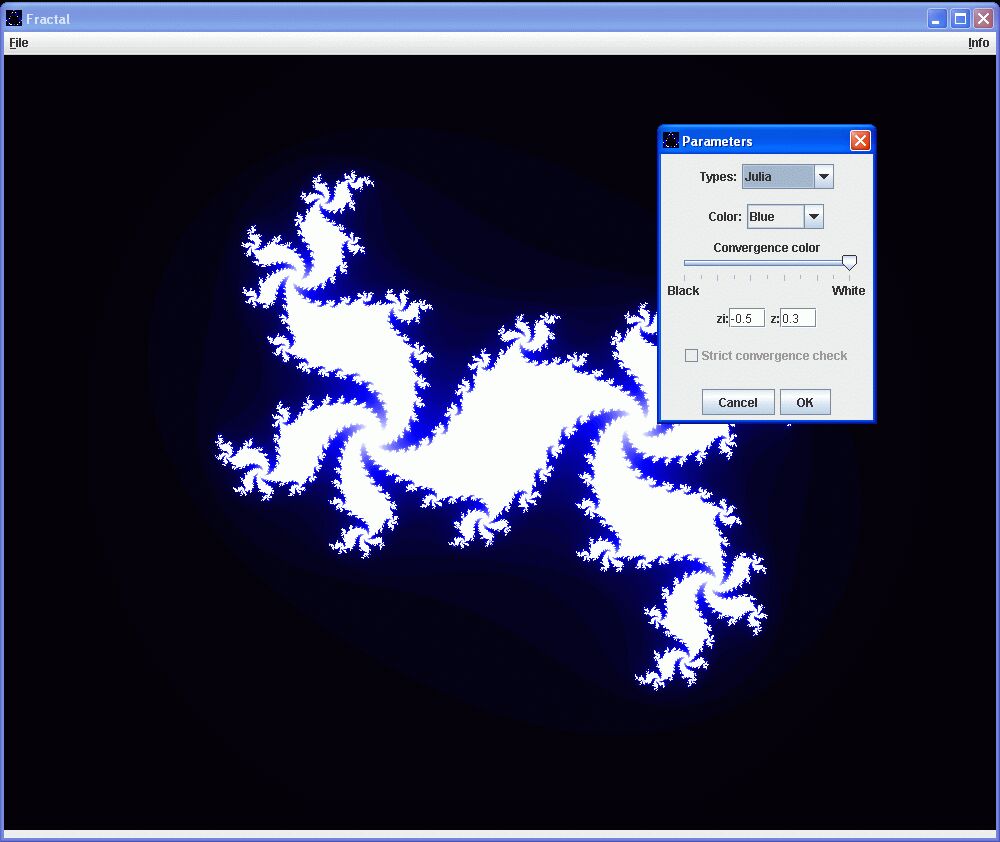

Download

Voraussetzung für das Programm ist Java 1.5 (JRE 5.0 auswählen).
Download: Fractal